
In particular, if you could move on a spacelike trajectory, there would be observers who would insist that you are traveling backwards in time. What you don't see in this spacetime diagram is a slice representing "the universe at one fixed time," because that kind of thing is completely observer-dependent in relativity. "Spacelike" trajectories that leave the light cones simply aren't allowed in the conventional way of doing things. On a diagram in which time stretches vertically and space horizontally, the possible paths of light from any event define light cones, and physical particles have to stay inside these light cones. The problem Scott is alluding to is that, in relativity, it's the speed-of-light barrier that prevents particles (or anything) from zipping around and meeting themselves in the past - a closed loop in spacetime.
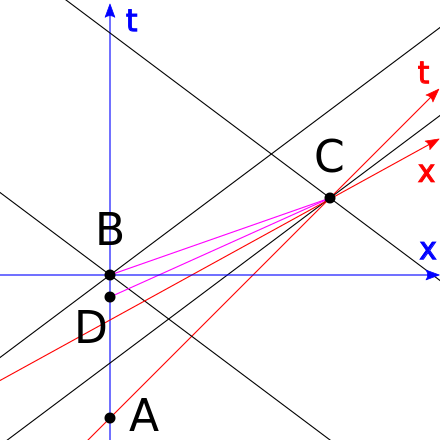
And I don’t understand how one could have tachyonic neutrinos without getting CTCs as well-would anyone who accepts that possibility be kind enough to explain it to me? Which of course led to questions, in response to one of which he commented thusly:Ĭlosed timelike curves seem to me to be a different order of strangeness from anything thus far discovered in physics-like maybe 1000 times stranger than relativity, QM, virtual particles, and black holes put together.

Back yet? Scott did foolishly at the end of the post mention the faster-than-light neutrino business. It's similar to one I've been contemplating myself, but more clever and original. Building in part on my talk at the time conference, Scott Aaronson has a blog post about entropy and complexity that you should go read right now.


 0 kommentar(er)
0 kommentar(er)
